Ellipse Area and Perimeter (Online Calculator)

Ellipses are intriguing geometric shapes that find applications in various fields, including mathematics, physics, and engineering. Understanding how to calculate their area and perimeter is essential for solving numerous problems accurately.

In this article, we’ll explore the fundamentals of ellipses, delve into the methods for determining their area and perimeter, and introduce our calculator, a valuable tool for performing these calculations seamlessly.

Understanding Ellipses

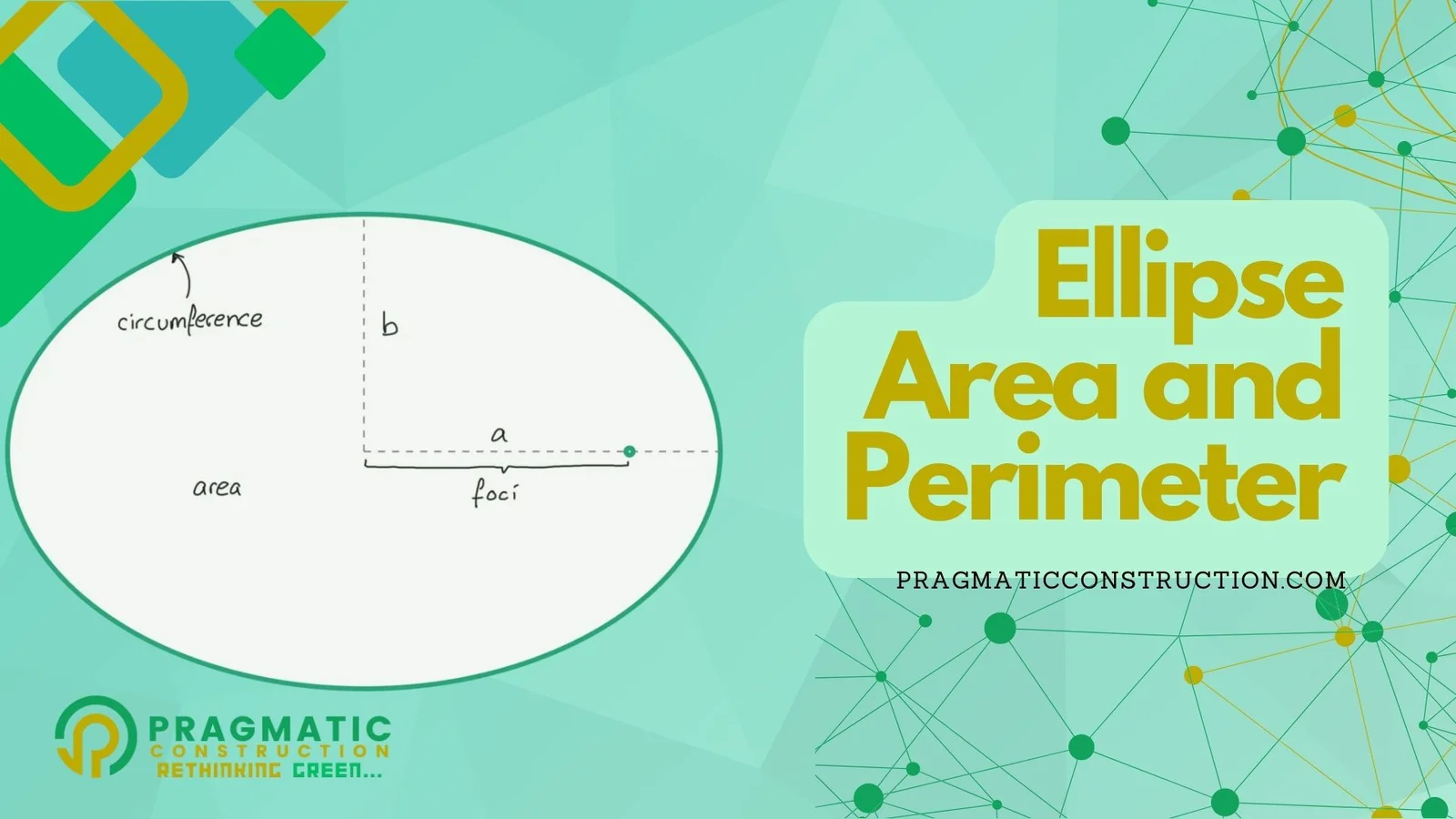
An ellipse is a closed curve resembling a squashed circle. It is defined by two foci and two axes: the major axis (the longest diameter) and the minor axis (the shortest diameter). The distance between any point on the ellipse and the two foci remains constant, making it a unique and versatile shape.

Calculating Area and Perimeter

To calculate the area (A) and perimeter (P) of an ellipse, we use specific formulas based on its dimensions. Given the lengths of the major axis (a) and minor axis (b), we can use the following formulas:

Area of an Ellipse (A) = π * a * b Perimeter of an Ellipse (P) ≈ π * (√(2 * (a^2 + b^2)))

These formulas provide accurate estimations of the area and perimeter of an ellipse, enabling precise quantification of its size and shape.

Ellipse Area and Perimeter Calculator

Our calculator is a powerful tool designed for efficiently computing the area and perimeter of ellipses. It allows users to input the dimensions of the major and minor axes, providing instant results for the corresponding area and perimeter values. With its user-friendly interface and precise calculations, our calculator simplifies complex mathematical tasks, empowering users to tackle challenges with confidence and accuracy.

Practical Applications

Mastering the calculations of area and perimeter for ellipses has practical implications across various disciplines. In architecture and engineering, it aids in designing structures with elliptical features, such as arches and domes.

In astronomy, ellipses are used to model the orbits of celestial bodies, providing insights into their movements.

Additionally, in mathematics and physics, ellipses serve as fundamental concepts in studying conic sections and trajectories.

Understanding Ellipse Perimeter:

In the realm of conic sections, an ellipse is a significant curve defined by two focal points and two radii: the semi-major axis and the semi-minor axis. The perimeter of an ellipse represents the total distance along its boundary. The major axis, being the longest chord of the ellipse, is complemented by the minor axis, which bisects the major axis perpendicularly. The formula for calculating the perimeter of an ellipse is:

Perimeter of an ellipse = 2π * √((r1^2 + r2^2) / 2)

Here, r1 and r2 denote the radii corresponding to the vertical and horizontal axes, respectively.

Important Information

Formula

A = ab/4 P = 𝛑R(1+(3H)/(10+√(4-3*H)))

where

A is the area of the ellipse a length of the short diameter

b length of the l diameter P the perimeter of the ellipse

𝛑 = 3.14159265

R = (a+b)/2 S = (a-b)/2 H = R²/S²

Conversions

one square foot ( ft²) = 144 square inches (in²)

one square inch (in²) = 0.00694444444444443 square feet (ft²)

one square foot ( ft²) = 0.09290304 square metres (m²)

square inch (in²) = 0.00064516 square metres (m²)

Different Examples

Example 1:

Given: Vertical radius (r1) = 5 units Horizontal radius (r2) = 3 units

Calculation Steps:

1. Area of the Ellipse (A): A = π * r1 * r2 A = π * 5 * 3 A ≈ 47.123 units²
2. Perimeter of the Ellipse (P): P ≈ π * √((r1² + r2²) / 2) P ≈ π * √((5² + 3²) / 2) P ≈ π * √((25 + 9) / 2) P ≈ π * √(34 / 2) P ≈ π * √17 P ≈ 15.409 units

Example 2:

Given: Vertical radius (r1) = 7 units Horizontal radius (r2) = 4 units

Calculation Steps:

1. Area of the Ellipse (A): A = π * r1 * r2 A = π * 7 * 4 A ≈ 87.964 units²
2. Perimeter of the Ellipse (P): P ≈ π * √((r1² + r2²) / 2) P ≈ π * √((7² + 4²) / 2) P ≈ π * √((49 + 16) / 2) P ≈ π * √(65 / 2) P ≈ π * √32.5 P ≈ 18.064
3. units

Example 3:

Given: Vertical radius (r1) = 10 units Horizontal radius (r2) = 6 units

Calculation Steps:

1. Area of the Ellipse (A): A = π * r1 * r2 A = π * 10 * 6 A ≈ 188.495 units²
2. Perimeter of the Ellipse (P): P ≈ π * √((r1² + r2²) / 2) P ≈ π * √((10² + 6²) / 2) P ≈ π * √((100 + 36) / 2) P ≈ π * √(136 / 2) P ≈ π * √68 P ≈ 26.081 units

Why is there no formula for the perimeter of an ellipse?

The perimeter of a shape is the total length of its boundary. For simple geometric shapes like circles and rectangles, there are well-defined formulas to calculate their perimeters.

However, when it comes to more complex shapes like ellipses, determining the perimeter is not as straightforward. Unlike a circle, which has a constant radius at every point along its circumference, an ellipse has varying distances between its boundary points and its foci.

This variability in distance makes it challenging to derive a single, simple formula for the perimeter of an ellipse.

One might wonder why it's not possible to find a formula analogous to the circumference formula for circles.

The reason lies in the nature of the ellipse itself. While a circle can be considered a special case of an ellipse with equal major and minor axes, the symmetry of a circle simplifies its perimeter calculation. In contrast, an ellipse lacks such symmetry, resulting in a more complex boundary shape.

Despite the absence of a straightforward formula, there are methods to approximate the perimeter of an ellipse.

One common approach involves using numerical integration techniques or series expansions to calculate the arc length of the ellipse's boundary.

Another method employs elliptic integrals, which are mathematical functions that arise in the study of elliptic curves and can be used to express the perimeter of an ellipse in terms of these integrals.

Overall, the absence of a simple formula for the perimeter of an ellipse highlights the geometric complexity of this shape and underscores the need for more sophisticated mathematical techniques to analyze and quantify its properties.

Half Ellipse Circumference Calculator

A half ellipse, also known as a semicircle, is a common geometric shape encountered in various contexts, from architectural design to engineering applications. Calculating the circumference of a half ellipse is essential for determining the length of curved structures such as arches and domes.

Fortunately, there are readily available tools, such as the Half Ellipse Circumference Calculator, that simplify this calculation process.

The Half Ellipse Circumference Calculator is an online tool designed to compute the circumference of a half ellipse based on the given dimensions of its major and minor axes.

Users can input the lengths of these axes into the calculator, and with a simple click, the tool instantly provides the corresponding circumference value. This calculator streamlines the calculation process, saving time and effort for users seeking accurate measurements for their projects.

To use the Half Ellipse Circumference Calculator, users follow these straightforward steps:

1. Input the length of the major axis (also known as the semi-major axis) into the designated field.
2. Input the length of the minor axis (also known as the semi-minor axis) into the corresponding field.
3. Click the "Calculate" button to initiate the computation.
4. The calculated circumference of the half ellipse is displayed, providing users with the desired measurement.

With its user-friendly interface and precise calculations, the Half Ellipse Circumference Calculator proves to be a valuable tool for architects, engineers, students, and anyone else requiring quick and accurate circumference values for half ellipse shapes.

Perimeter of Ellipse Integral

Calculating the perimeter of an ellipse poses a mathematical challenge due to the shape's asymmetry and the varying distances between its boundary points and foci. While no simple formula exists for determining the perimeter, mathematical techniques such as integration offer a means to approximate this value.

One method for calculating the perimeter of an ellipse involves using elliptic integrals, which are mathematical functions used to express the arc length of elliptic curves. By integrating the differential element along the ellipse's boundary, one can obtain an expression for the arc length and, consequently, the perimeter.

The general form of the integral for the perimeter of an ellipse is:

P = 4a ∫[0 to π/2] √(1 - e^2 sin^2 θ) dθ

where:

• P represents the perimeter of the ellipse.
• a is the length of the semi-major axis.
• e is the eccentricity of the ellipse, defined as e = √(1 - (b^2 / a^2)), where b is the length of the semi-minor axis.
• θ is the parameter representing the angle along the ellipse's boundary.

This integral represents the arc length of the ellipse's quarter segment in the first quadrant.

Multiplying by 4 yields the total perimeter of the ellipse. However, evaluating this integral analytically is challenging, and numerical integration techniques are often employed to approximate the perimeter.

While the perimeter of an ellipse does not have a simple, closed-form expression like that of a circle, mathematical tools such as integration provide a means to calculate it accurately, highlighting the intricate nature of geometric curves and the versatility of mathematical techniques in solving complex problems.

Conclusion

Ellipses are versatile geometric shapes with diverse applications in science, engineering, and mathematics. By understanding how to calculate their area and perimeter, individuals gain valuable insights into their properties and behaviors. With our calculator, performing these calculations becomes a seamless and efficient process, enabling users to explore the rich possibilities of ellipses with ease. Whether in academic studies, professional projects, or personal interests, mastering ellipses enhances problem-solving skills and fosters a deeper appreciation for the beauty of mathematics and geometry.