Percent Slope to Degrees – Slope Percentage Calculator (Free)

In various fields such as construction, engineering, geography, and even in everyday life, understanding slopes is crucial. Slopes are a measure of the steepness of a surface, often expressed as a percentage or an angle.

While slope percentage provides a direct indication of the incline, sometimes it’s more intuitive to think in terms of angles. In this detailed exploration, we delve into the conversion of slope percentage to angles in degrees using the arctangent function.

We will cover the mathematical foundation, the practical applications, and the significance of this conversion in different contexts.

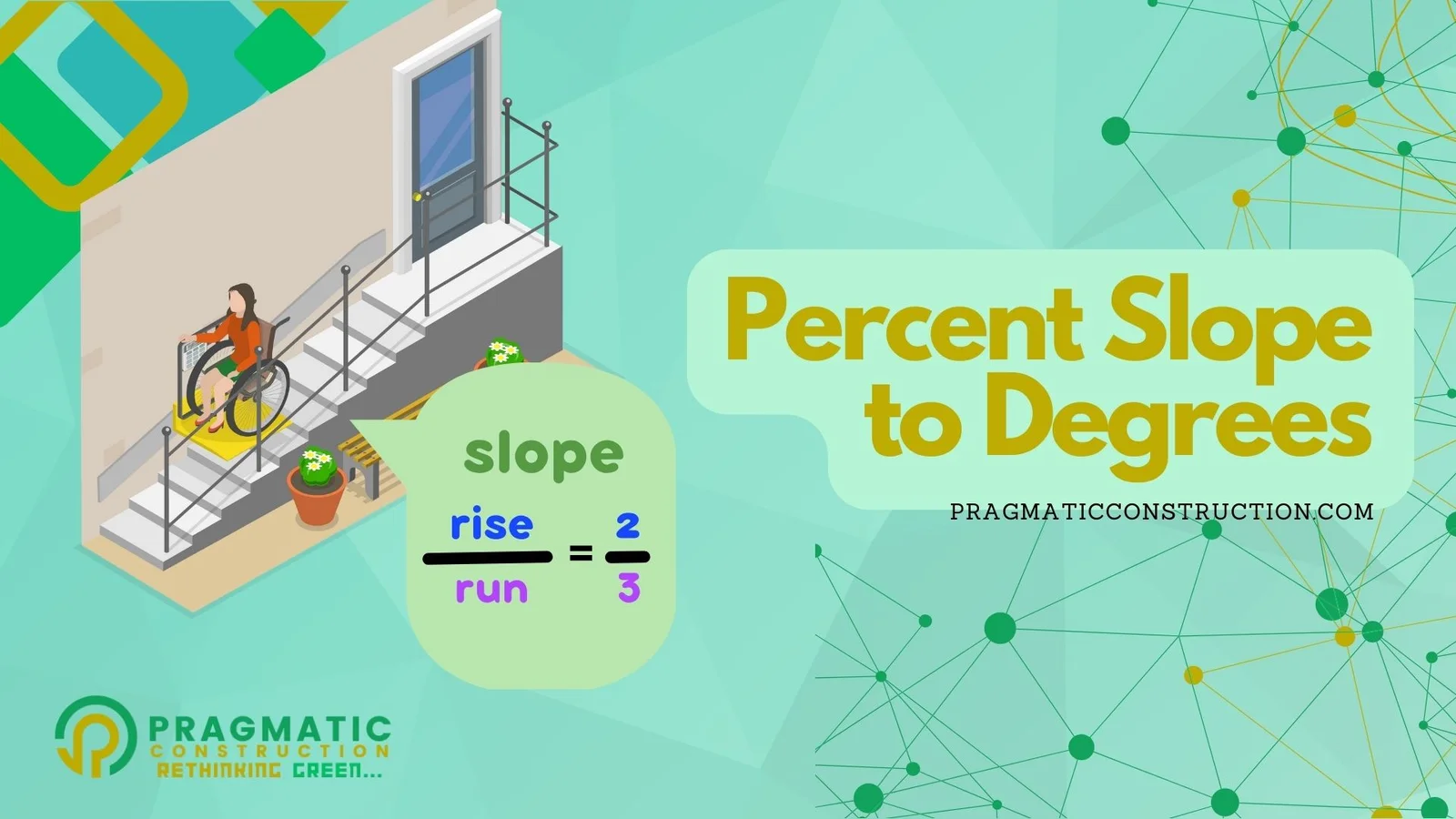
Slope Percentage to Angle in Degrees

To facilitate quick and accurate conversions, a slope percentage to angle calculator can be a valuable tool. This calculator allows users to input the slope percentage and specify the desired decimal precision, providing results in both degrees and radians.

Let’s explore the features and functionality of this calculator in detail.

Features of the Calculator:

1. Input Fields:
   • Slope Percentage: Users can enter the slope percentage they wish to convert. This input field allows for any percentage value, positive or negative.
   • Decimal Precision: Users can specify the desired precision for the results, indicating the number of decimal places they want in the output for both degrees and radians.
2. Results Display:
   • Radians: The calculator provides the angle in radians as the result of the conversion. Radians are a unit of angular measurement used in mathematics and physics, particularly in trigonometry.
   • Degrees: Alongside radians, the calculator displays the angle in degrees. Degrees are a more commonly used unit of angular measurement in everyday contexts.

Understanding Slope Percentage

Slope percentage is a common way to express the steepness of a slope. It represents the ratio of the vertical rise to the horizontal run, multiplied by 100 to get a percentage. For instance, a slope of 20% means that for every 100 units traveled horizontally, there is a rise of 20 units vertically. Slope percentage is widely used in construction, road engineering, landscaping, and other fields where understanding terrain is essential.

Some aspects of Trigonometry Relevant to Slope Percentage Concept

Trigonometry, a branch of mathematics, deals with the relationships between the angles and sides of triangles. One fundamental concept in trigonometry is the trigonometric functions, which relate the angles of a right triangle to the lengths of its sides. The primary trigonometric functions include sine, cosine, tangent, cosecant, secant, and cotangent.

Arctangent Function

The arctangent function, often denoted as atan or tan^(-1), is the inverse of the tangent function. It takes a ratio of the length of the side opposite an angle to the length of the side adjacent to the angle and returns the measure of the angle. In simpler terms, given the ratio of two sides of a right triangle, the arctangent function gives us the angle corresponding to that ratio.

Conversion from Slope Percentage to Angle

To convert a slope percentage to an angle in degrees, we utilize the arctangent function. The formula for this conversion is straightforward: atan(percentage ÷ 100). By dividing the slope percentage by 100 and then applying the arctangent function, we obtain the angle in radians. To convert this angle to degrees, we use the fact that 1 radian is approximately equal to 57.2958 degrees.

Example Calculation

Let’s consider an example calculation to understand the process better. Suppose we have a slope percentage of 42%. To convert this to degrees, we apply the formula: atan(42 ÷ 100) = atan(0.42) ≈ 22.9°. This means that a slope of 42% corresponds to an angle of approximately 22.9 degrees.

Significance of Slope Angle: Understanding slope angles provides valuable insights in various applications. In construction and civil engineering, knowing the angle of a slope helps in designing safe and stable structures. For example, when building roads or railways, engineers need to ensure that the slopes are within safe limits to prevent landslides or structural failures. In landscaping and agriculture, slope angles influence water drainage, erosion control, and crop selection.

Practical Applications Converting Slope Percentage to Angle in Degrees

The conversion from slope percentage to angle in degrees finds practical applications in several fields:

1. Architecture and Construction: Architects and engineers use slope angles to design ramps, stairs, and wheelchair-accessible pathways in buildings. By converting slope percentages to angles, they ensure that the inclines meet safety standards and provide accessibility for all individuals.
2. Road Design: Civil engineers rely on slope angles to design roads with appropriate gradients. Steep slopes can pose challenges for vehicle traction and braking, especially in adverse weather conditions. By converting slope percentages to angles, engineers can determine the optimal road gradients for safe and efficient transportation routes.
3. Land Surveying: Surveyors use slope angles to assess the topography of land parcels. By measuring slope angles at various points, they can create contour maps that depict the terrain’s elevation changes. This information is essential for urban planning, environmental management, and land development projects.
4. Outdoor Recreation: Slope angles play a crucial role in outdoor recreation activities such as hiking, skiing, and mountain biking. Trail designers consider slope angles to create routes that are both challenging and safe for enthusiasts. By converting slope percentages to angles, they can design trails with suitable inclines for different skill levels.

Mathematical Foundation

The conversion from slope percentage to angle in degrees relies on trigonometric principles.

Let’s explore the mathematical foundation behind this conversion:

Consider a right triangle where one angle is θ (theta), the opposite side is O, and the adjacent side is A. According to trigonometry:

• Tangent (tan θ) = Opposite / Adjacent.

Using this relationship, if we know the slope percentage, which is the ratio of the opposite side (rise) to the adjacent side (run), we can find the angle θ using the arctangent function:

θ = atan (Opposite / Adjacent).

In the case of slope percentage, the opposite side represents the vertical rise, and the adjacent side represents the horizontal run. By substituting these values into the arctangent formula and simplifying, we obtain the angle in radians. To convert this angle to degrees, we multiply by the conversion factor: 180/π radians ≈ 57.2958 degrees.

Real-world Examples

Let’s explore some real-world examples where the conversion from slope percentage to angle in degrees is applied:

1. Road Construction: When designing roads, engineers must adhere to specific slope angle limits to ensure safety and stability. For example, highways typically have gentle slopes with angles ranging from 1% to 6%, while mountain roads may have steeper slopes up to 10% or more. By converting slope percentages to angles, engineers can determine the most suitable gradients for different road segments.
2. Roofing: In roofing construction, slope angles dictate the type of roofing materials and drainage systems used. Steeper roofs require materials that can withstand higher wind loads and provide better water runoff. By converting slope percentages to angles, roofing contractors can accurately assess the pitch of a roof and recommend appropriate roofing solutions.
3. Agricultural Practices: Farmers consider slope angles when planning irrigation systems and crop layouts. Slopes influence water distribution, soil erosion, and crop productivity. By converting slope percentages to angles, farmers can design terraces, contour ditches, and drainage channels to optimize water management and soil conservation efforts.

Limitations and Considerations

While converting slope percentages to angles using the arctangent function provides valuable insights, it’s essential to acknowledge some limitations and considerations:

1. Assumes Right Triangle: The conversion formula assumes that the slope forms a right triangle with the horizontal ground. In reality, slopes may have irregular shapes or complex terrain features that deviate from this idealized model. In such cases, additional surveying techniques and computational methods may be required to accurately measure slope angles.
2. Local Variations: Slope angles can vary significantly depending on local topography, geological conditions, and human activities. For example, natural slopes in mountainous regions may have steeper angles compared to slopes modified by human intervention, such as terracing or excavation. When interpreting slope angle data, it’s essential to consider these local variations and site-specific factors.
3. Measurement Errors: The accuracy of slope angle measurements depends on the precision of the slope percentage data and the surveying instruments used. Measurement errors, such as inaccuracies in elevation readings or instrument calibration, can affect the reliability of slope angle calculations. Surveyors should employ rigorous quality control procedures to minimize errors and ensure data integrity.

Conclusion

The conversion from slope percentage to angle in degrees using the arctangent function is a fundamental concept with diverse applications in various fields.

By understanding the mathematical principles behind this conversion, professionals in construction, engineering, geography, and other disciplines can effectively analyze terrain characteristics, design infrastructure, and make informed decisions.

While this conversion provides valuable insights, it’s essential to consider its limitations and complement it with additional surveying techniques and computational tools for accurate slope analysis.

Overall, the ability to convert slope percentages to angles enhances our understanding of slope dynamics and contributes to the sustainable management of natural and built environments.